- 18/02/22 08:39
- INTA Copernicus Relay
En observación de la Tierra es muy frecuente trabajar con datos espacial o temporalmente incompletos, ya que la cobertura nubosa nos impide obtener datos regularmente. Hay muchas alternativas para intentar estimar los datos perdidos por la presencia de nubes, alternativas que dependen del objetivo del trabajo y del tipo de datos disponibles.
Nosotros estamos probando ahora, en el marco de nuestro proyecto STERNA con Puertos del Estado, un método basado en Empirical Orthogonal Functions (EOF). Seguimos para ello el desarrollo del grupo GHER de la Universidad de Lieja, publicado en numerosas ocasiones, como este trabajo de Alvera-Azcárate et al.. Este desarrollo se ha implementado en una herramienta llamada DINEOF (Data Interpolation with Empirical Orthogonal Functions) que está disponible vía github.
La base del método es la habitual para EOF. Se construye una tabla de observaciones donde cada fila es un punto observable (por ejemplo una boya oceanográfica de las utilizadas en STERNA) y cada columna una medición distinta de una variable a estudiar (en este caso la SST determinada por Sentinel-3 para cada fecha). El análisis de la descomposición en valores singulares de la matriz así formada permite hallar patrones que describen la manera en que se comporta la variable medida entre puntos y a lo largo del tiempo. En el caso de la temperatura del mar, estamos descubriendo cómo se relaciona la variación de temperatura en un píxel y fecha con otros píxeles y fechas.
Si la tabla es suficientemente representativa de la variable estudiada, aunque tenga missing data (como ocurre bajo las nubes), las EOF (los "autovectores" espaciales y temporales de la matriz) son capaces de hallar los patrones subyacentes. Y una vez conocidos, se puede estimar el valor esperable según fecha y posición, y rellenar así los huecos. Y sin necesidad de información a priori.
DINEOF utiliza este principio, empezando con una estimación de la variable en los puntos no disponibles, probando con diferente número de vectores (los menos posibles) y trabajando iterativamente hasta encontrar un valor que minimice el error en una serie de puntos de control.
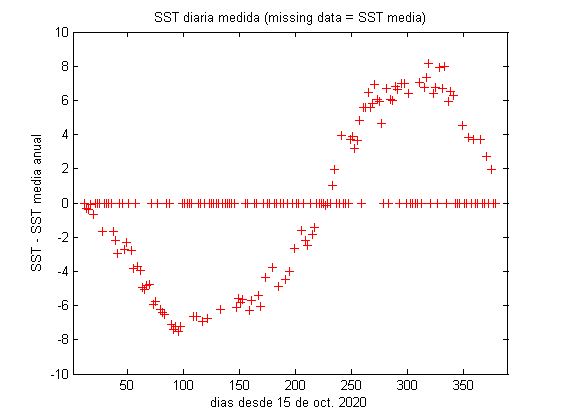
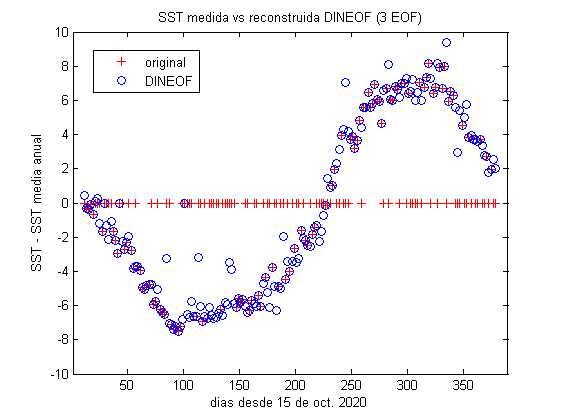
En las figuras os mostramos un ejemplo del uso de DINEOF con una serie temporal de imágenes SST de Sentinel-3. La figura superior muestra los valores para un ciclo anual para un punto en la costa de Valencia (recordando que DINEOF debe trabajar sobre un conjunto de datos espaciales, no un punto único). Cuando no hay dato disponible (típicamente por nubes) asignamos la SST media, y por tanto el valor en el eje Y es 0. Esto permite visualizar esos missing data, casi el 50% del conjunto. Tras aplicar DINEOF reconstruyendo la matriz de datos solo con los 3 primeros vectores (EOFs), vemos en la figura inferior que la mayor parte de los datos a 0 se mueven a su valor esperado. También vemos que un par de datos se quedan incorrectamente en el valor inicial, y que otros se estiman probablemente demasiado por encima o debajo del valor esperado. Pero el conjunto es muy prometedor.
El número de EOFs considerado, el criterio para detener las iteraciones y el valor inicial en los missing data forman el conjunto de parámetros que debe ajustarse para cada aplicación, dando a DINEOF flexibilidad y potencial. Y es lo que nosotros tenemos que afinar todavía para el caso de STERNA.